# The Rule of Threes
The number three is a special number in game design — in everything, really. It crops up everywhere: three talent trees, three rounds, three party members, etc.
I don’t care what you are designing, if you can break things down, divide things up, or cut things out so that it gets you down to threes, then it is a good decision. Your game will, in all likelihood, be better for it. That’s a promise. It will feel rough, but the player doesn’t know what you cut from your game - they only know the product.
The Rule of Three is so universal and applicable that it will probably be the greatest trick in your toolbox for a long time. People will marvel at your ability to create simple, clean, elegant systems, and little will they know that all you did was focus on Three.
The number three crops up in all different kinds of fields:
- Photography – Rule of Thirds
- Writing – Rule of three
- Economics – Rule of Three
- Project Estimations – Even how you estimate your time if often off by a factor of 3
But I admit, at times it won’t feel right to break things down to threes, and that’s where his two friends come into play: Two and Five.
There is just something about systems in Twos, Threes, and Fives. They just feel RIGHT. You feel like you have choice, but you are not overwhelmed. You will notice, of course, that these are Fibonacci numbers — 2, 3, 5 — which is NOT a coincidence.
I have a simple rule I follow when designing systems. If I need to add more options to a system, the number of options provided has to a Fibonacci Number. Here’s why: once you provide five options to the player it can be super easy to say, “why not six?” Sure, why NOT six. Well, because it bloats the game! More is not always better; in fact, your game is almost always worse with the additional weight of these options.
Constraining myself to the Fibonacci sequence forces me to REALLY commit to “just one more”, as now it is NOT just one more, but in fact several more.
If, for example, I currently provide five options, then I would have to upgrade it to eight; if I have eight, then it must become thirteen. The choice to increase the player’s options, as you can clearly see, gets heftier and heftier: THERE’S A LESSON THERE.
For other examples of why you would use this type of rule, check out the articles:
# A Real World Example
When I was designing the Challenge Tower for MK9 I was faced with a compelling set of problems.
- The player should have 300 completely different missions
- They needed to get money for beating them
- They should be able to buy their way passed missions they didn’t like
- It needed to all fit into the larger picture of the entire economy.
The first question was how to break up the missions. I decided on blocks of 5 missions that focused on the same character. This way I could ramp up the difficulty on a player, and they are given enough time to familiarize themselves with how that character controls. Between each block would be a minigame, which breaks up the gameplay to keep things interesting.
I also had some special or funny missions that I wanted to showcase, and doing it this way meant I could have a cool mission every 30 missions.
Once I had everything broken up into my mission blocks, I began the next phase of the process, which was to systematically rank them on how difficult they were on a scale of 1 to 5. It is difficult to do this kind of estimation in a vacuum, by the way, so make good use of other people. You are always going to be the worst judge of your own difficulty spikes.
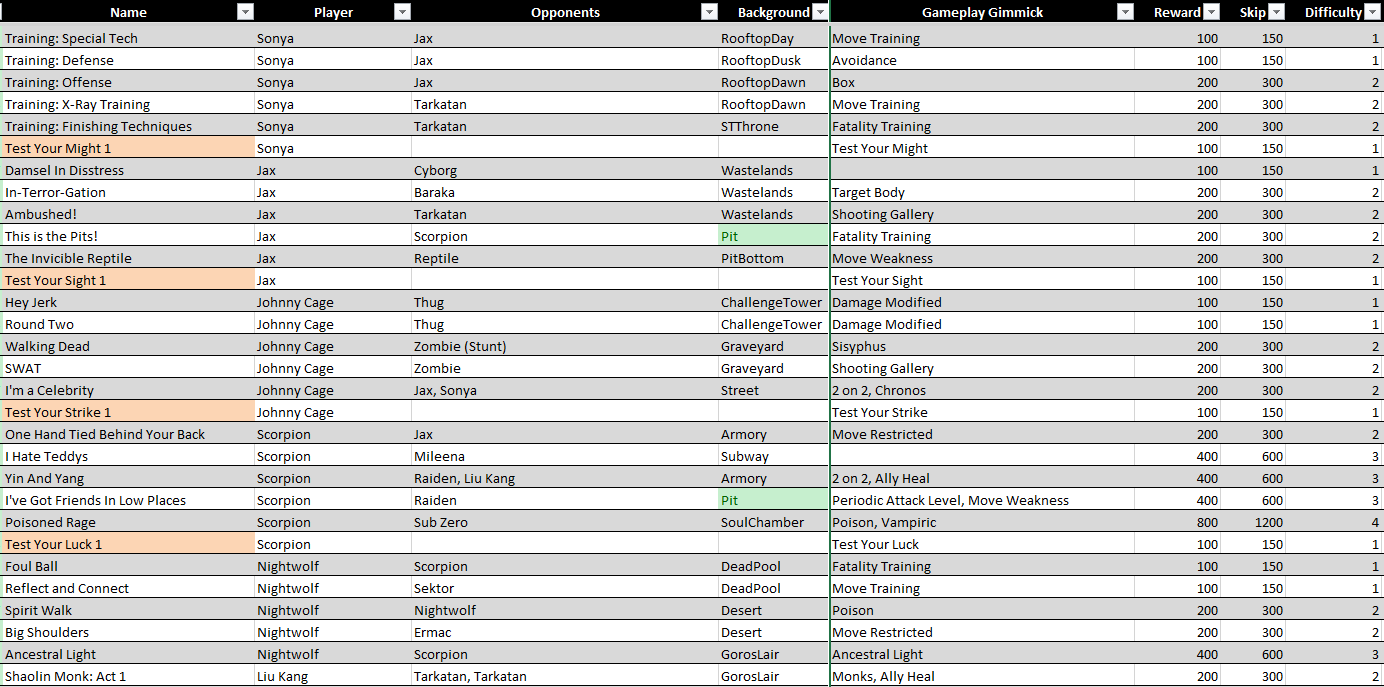
As an aside, I was also tracking the kind of gameplay gimmicks being used, how many times different characters occurred, what arenas it took place in, what kind of ring knockouts used, etc. Missions were constantly being shuffled around, and keeping this file maintained was a full time and commitment heavy job, but it was so worth it.
Finally, now that I had all the missions organized and categorized, I was ready to start assigning reward values to them, which, using the 5 point difficulty scale I already created, was output from the following formula:
Reward = 50 * (2 ^ Difficulty)
This gave me nice round numbers that started off at 100. The final outcome looks random, but you can see that at every step of the process I was making meaningful calls about how things were organized, and, more importantly, you probably noticed the constant appearance of 2, 3, and 5 in the design. That was all on purpose.